D_e 為所有施工階段的最大開挖深度，下方支撐軸力資料表中的 D_e1' 及 D_e2' 為該施工階段的開挖深度。

當支撐條件輸入方式採用自動載入分析結果時，系統會自動載入 D_e。若支撐條件輸入方式採用手動輸入時，D_e 需由使用者自行輸入。

L₁ + L_o 代表中間柱型鋼之有效無側撐長度。

當支撐條件輸入方式採用自動載入分析結果時，系統會自動找出開挖至大底階段的 PHASE，並填入相對應的 L₁ 及支撐軸力，使用者亦可自行調整 PHASE 數值，L₁ 及相對應的支撐軸力會自動更新。

若支撐條件輸入方式採用手動輸入時，L₁ 需由使用者自行輸入；或需要手動輸入時，L₁，請切換支撐條件輸入方式為手動輸入。注意，程式自動計算的 L₁ 為各開挖階段支撐、樓板或底板到該階段開挖面的距離，因此大底 PC 的至開挖面的深度也會用來計算 L₁，此時 L₁ 會很小，如果設計者想要忽略大底 PC，請切換支撐條件輸入方式為手動輸入，並自行修改 L₁。

至於 L_o 則由程式依輸入條件自動計算取得。

型鋼頂端不一定與地表等高，型鋼頂端低於地表時 H_o 取正值，反之取負值。中間柱自重 N₄ 與 H_o 及 D_e 有關：

$$\mathrm{N_4=w_D×(D_e-H_o)×r}$$

當中間柱與覆工系統共用時，N₅ 應考慮覆工系統所可能承受之各項荷重，包括靜荷重、堆置荷重、交通荷重及吊掛管線荷重等。

當中間柱施工不完善，或中間柱與擋土壁發生不均勻沉陷，亦或因支撐施工誤差，導致支撐與中間柱未能完全正交時，支撐軸力將對中間柱產生額外的下壓或拉拔作用力。該作用力可依下式計算：

$$\mathrm{N_1=n×(P+P_t)×r}$$

其中，支撐傾斜力比值 r 為經驗值，根據現地統計資料及設計經驗，r 通常取約 2%。使用者亦可依實際設計需求，調整採用其他適當數值。

自動載入分析結果

使用者可直接匯入 XDO、RIDO 或 TORSA 計算書中的分析結果，系統會自動擷取各施工階段的分析支撐軸力、支撐深度、開挖深度及分析間距，自動分析支撐與開挖面最大距離的施工階段，並套用至表格，其餘必要參數則由系統以常用設計值預先填入，快速建立中間柱檢核所需之資料初稿。若為 XDO 計算書，系統則可額外再擷取支撐型鋼型號。

自動載入分析結果請點選上方 按鈕，支撐配置為雙向支撐時，可針對不同方向分別載入不同之分析檔案，亦可選擇載入相同檔案。

手動輸入

使用者可自行輸入支撐型鋼型號、支撐深度、支撐軸力、支撐溫度力......等資料，適合非採用前述開挖擋土分析軟體之情境。

中間柱最不利之受力狀態通常發生於最下階支撐與開挖面距離最大之階段。於檢核中間柱安全性時，除應考慮其所承受之軸力外，尚須評估最下階支撐荷重偏心所產生之彎矩對中間柱穩定性的影響。該偏心彎矩之計算方式及傳遞方向，除了與支撐荷產生之下壓力有關之外，將隨最下階支撐之配置條件而異，例如：支撐配置 (單向或雙向)、支撐路數 (單支撐或雙支撐) 以及支撐與中間柱之連結方式等因素，而設計考量模式不同也會影響偏心彎矩之計算方式。

為便於後續敘述，先定義 F₁ 及 F₂ 分別代表①方向及②方向最下階支撐造成之下壓力，包括：支撐軸力及溫度力對中間柱產生額外的下壓力、支撐的靜荷重及活載重；e_x 代表①方向支撐對中間柱強軸的偏心距，e_y 代表②方向支撐對中間柱弱軸的偏心距，M_x 及 M_y 分別代表中間柱強軸及弱軸的偏心彎矩。

當最下階支撐採用單支撐時，偏心彎矩計算方式有以下三種情況：

強軸方向

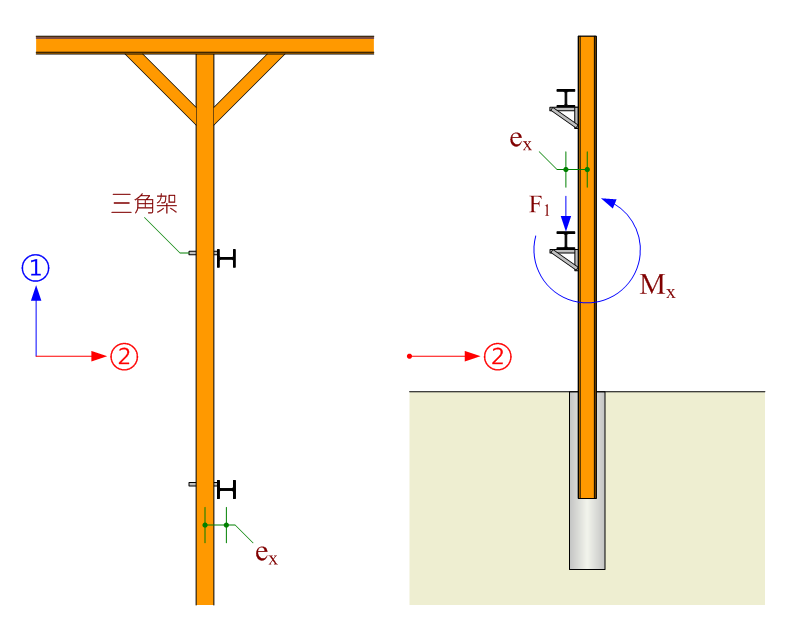
在單向支撐配置下，①方向支撐跨接於三角架上，且三角架固定於中間柱單一翼板時，支撐對中間柱產生之下壓力 F₁ 將對中間柱之強軸產生彎矩。

$$\mathrm{M_x=F_1×e_x}$$

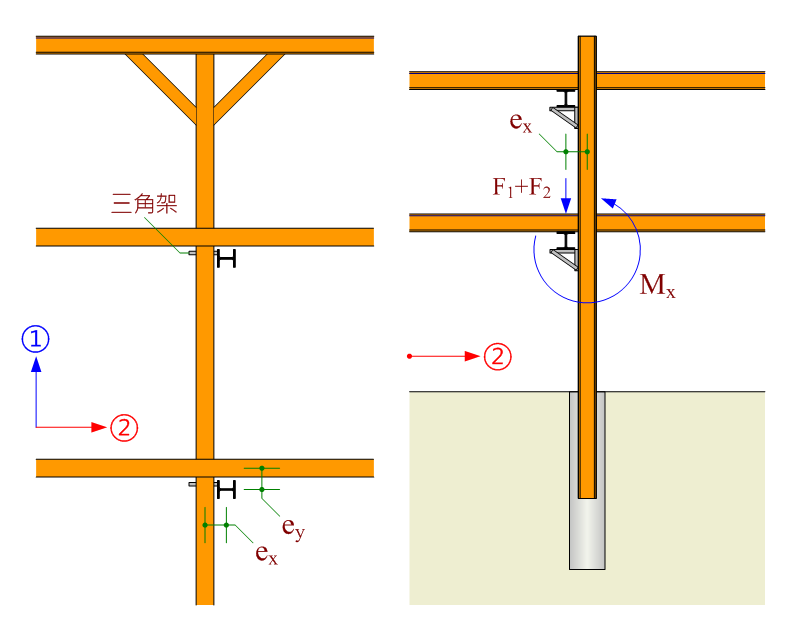
在雙向支撐配置下，②方向上層支撐橫跨於①方向下層支撐，F₂ 經由①方向下層支撐傳遞至三角架，F₁ 及 F₂ 同時對中間柱之強軸方向產生彎矩。

$$\mathrm{M_x=(F_1+F_2)×e_x}$$

弱軸方向

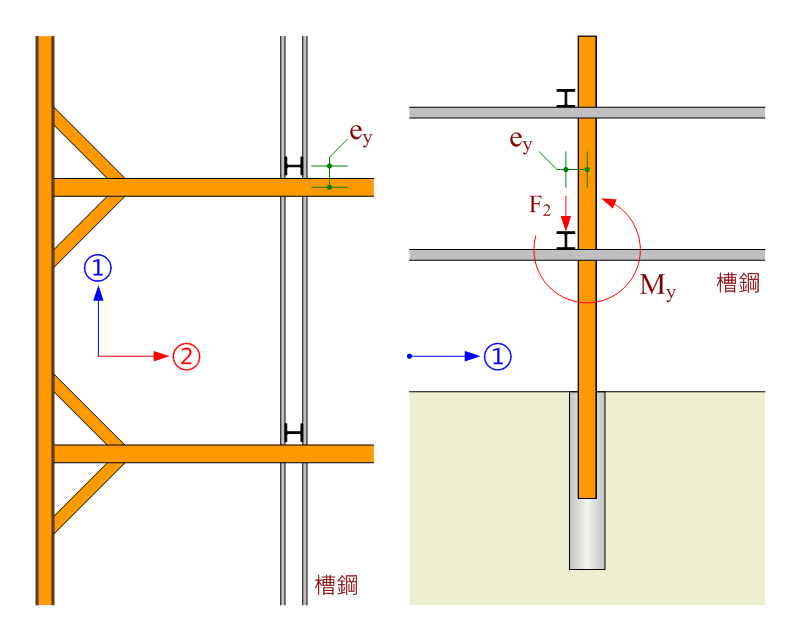
在單向支撐配置下，②方向支撐跨接於一對槽鋼上，且槽鋼分別固定於中間柱兩側翼板時，F₂ 將對中間柱之弱軸產生彎矩。

$$\mathrm{M_y=F_2×e_y}$$

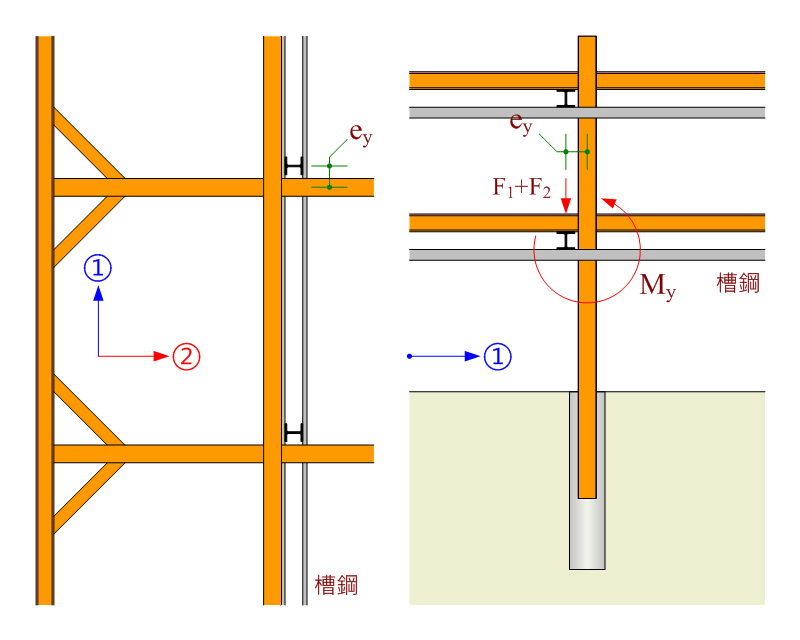
在雙向支撐配置下，①方向上層支撐之下壓力經由②方向下層支撐傳遞至槽鋼，F₁ 及 F₂ 同時對中間柱之弱軸方向產生彎矩。(註：實務上一般建築案雙向支撐採用槽鋼連結中間柱的情況較為少見，捷運案常採用。)

$$\mathrm{M_y=(F_1+F_2)×e_y}$$

個別傳遞

因支撐與中間柱施工接合特性考量，在雙向支撐的情況下，F₁ 對中間柱強軸產生彎矩，F₂ 對中間柱弱軸產生彎矩。

$$\mathrm{M_x=F_1×e_x}$$ $$\mathrm{M_y=F_2×e_y}$$

當最下階支撐採用雙支撐時，通常假設中間柱兩側支撐所產生之偏心荷重可相互抵銷，因而不致對中間柱造成彎矩。

然而業界亦有保守設計作法，認為仍應考量雙支撐中之單側支撐下壓力可能對中間柱造成偏心彎矩之影響。採用此保守考量時，偏心彎矩計算方式有以下三種情況：

強軸方向

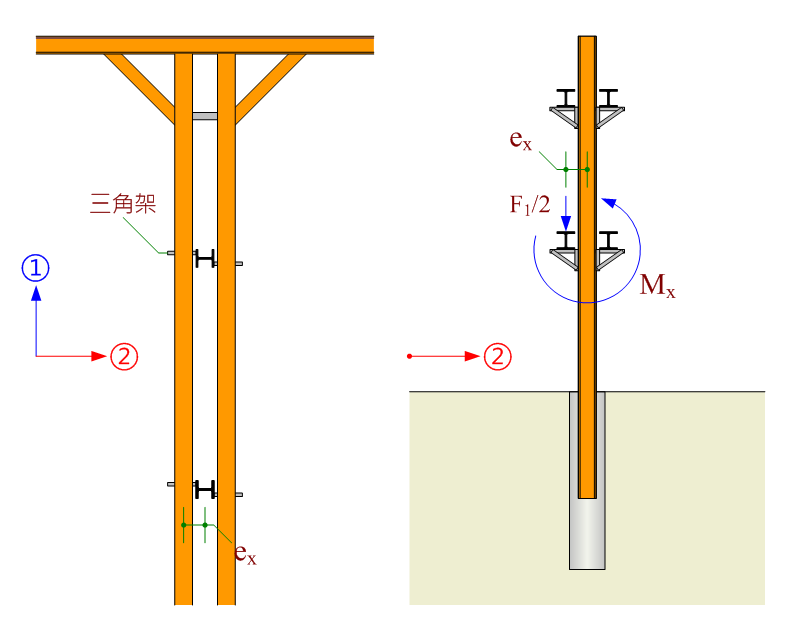
在單向支撐配置下，①方向支撐 (雙支撐) 經由三架角與中間柱兩側翼板連結，F₁ 為雙支撐對中間柱產生之下壓力總合，計算彎矩時因僅考量單側支撐，F₁ 需折半。

$$\mathrm{M_x=\frac{F_1}{2}×e_x}$$

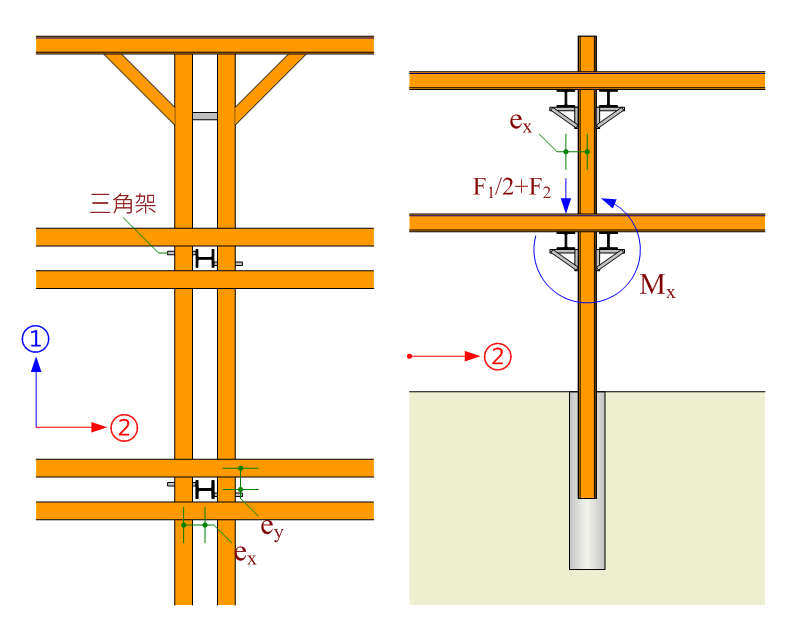
在雙向支撐配置下，②方向上層支撐橫跨於①方向下層支撐，F₂ 由①方向下層支撐 (雙支撐) 之單側透過三角架對中間柱之強軸方向產生彎矩。

$$\mathrm{M_x=(\frac{F_1}{2}+F_2)×e_x}$$

弱軸方向

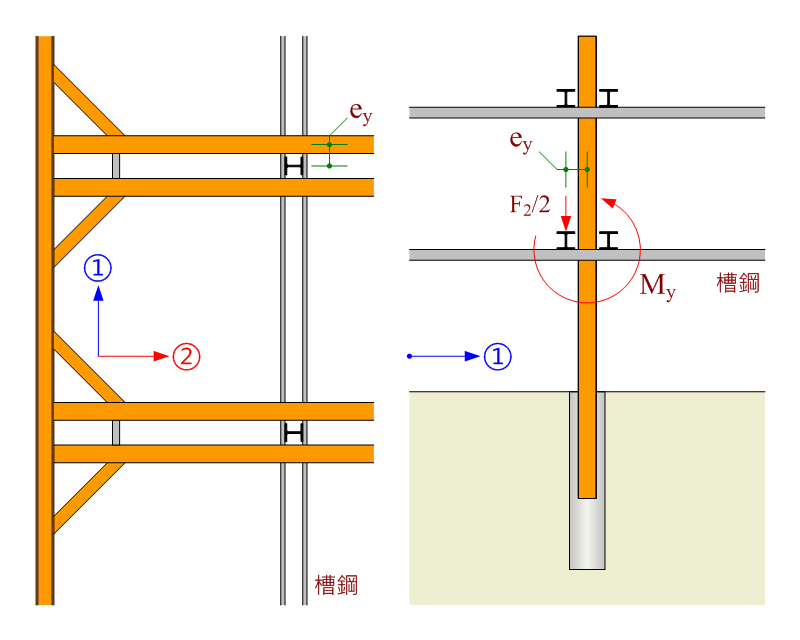
在單向支撐配置下，②方向支撐 (雙支撐) 經由槽鋼與中間柱連結，F₂ 為雙支撐對中間柱產生之下壓力總合，計算彎矩時因僅考量單側支撐，F₂ 需折半。

$$\mathrm{M_y=\frac{F_2}{2}×e_y}$$

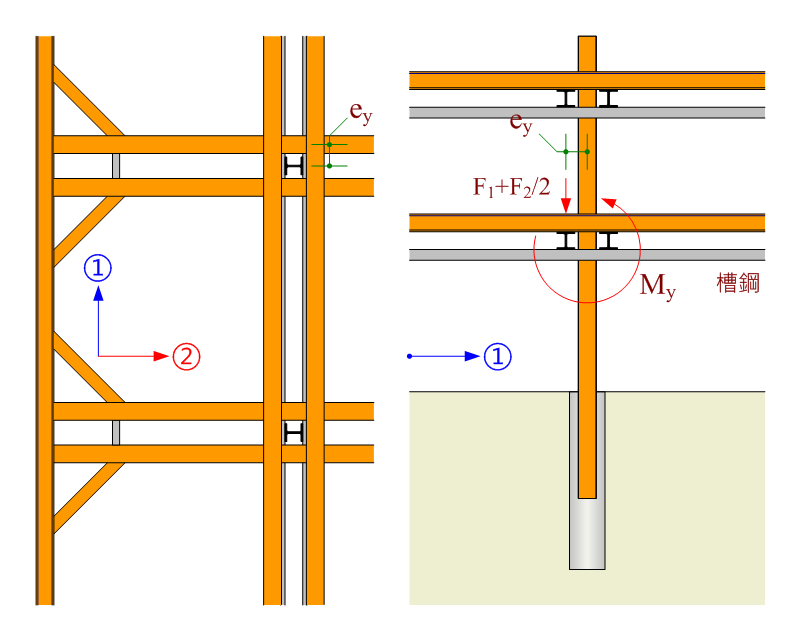
在雙向支撐配置下，①方向上層支撐橫跨於②方向下層支撐，F₁ 經由②方向下層支撐 (雙支撐) 之單側透過由槽鋼對中間柱之弱軸方向產生彎矩。

$$\mathrm{M_y=(F_1+\frac{F_2}{2})×e_y}$$

個別傳遞

因支撐與中間柱施工接合特性考量，①方向支撐 (雙支撐) 之單側支撐下壓力對強軸產生彎矩，②方向支撐 (雙支撐) 之單側支撐下壓力對弱軸產生彎矩，計算彎矩時因僅考慮單側支撐，F₁ 及 F₂ 需折半。

$$\mathrm{M_x=\frac{F_1}{2}×e_x}$$

$$\mathrm{M_y=\frac{F_2}{2}×e_y}$$

CATii 提供三種基樁承載力決定方式，分別說明如下。

輸入基樁承載力

使用者可以另外利用 CATii「單樁軸向分析」來計算基樁承載力，或自行以其他方式估算，再將基樁承載力輸入。採用本方法仍需輸入基樁範圍平均 SPT-N 值 N_avg，做為求取中間柱下方假設支點深度 L_o 之用。

輸入簡化單一地層參數

輸入基樁範圍之 N_avg，CATii 自動求出基樁容許承載力。本方法僅適用砂質地層。

輸入所有地層參數

輸入完整的地層參數及其他基樁分析條件，CATii 自動求出基樁容許承載力。

參考「鋼骨鋼筋混凝土結構設計實例」，型鋼與混凝土間之長期容許握持應力可以取 0.02f_c'，本程式以此為預設值。使用者亦可自行決定採用其他設計數值。

參考 RC 設計規範 TWN-USD100 G.4 節，型鋼容許承載應力可以取 0.3f_c'，本程式以此為預設值。使用者亦可自行決定採用其他設計數值。

當基樁貫入岩盤內時，CATii 採用以下公式計算基樁在岩層中之摩擦力及承載力。

岩層摩擦力

樁身與岩層界面之單位面積摩擦力可根據 Horvath et. al (1983) 所建議之公式估算：

$$\mathrm{f_s=\lambda\sqrt{q_u}}$$

上式中，λ 為經驗值，約介於 2~3\(\mathrm{\sqrt{tf/m^2}}\) 之間，q_u 為設計岩石單壓強度 (tf/m²)。

岩層承載力

單位面積極限承載力可由 Goodman (1980) 所建議之公式估算：

$$\mathrm{q_b=q_u(N_ϕ+1)}$$ $$\mathrm{N_ϕ=tan^2(45+ϕ'/2)}$$

當樁基礎承載於均質砂性地層時，早期之設計常假設支承力隨樁基之埋置深度而線性增加，惟根據近年來之研究顯示，樁端極限支承力 q_b 與樁身摩擦力 f_s 於超過某一埋置深度時有趨近某一定值之現象，Vesic (1963) 將此深度定義為臨界深度，CATii 採用 L_pcr 做為臨界深度符號。

綜合文獻研究結果顯示，L_pcr 之變化範圍極廣，約介於 4D~60D 之間，主要與地層之摩擦角值及基樁施工方式有關，目前國內之試樁資料仍未完備，現階段建議採 NAVFAC DM-7.2 (1982) 規範所建議之 20D 為臨界深度，超過此深度時，其有效覆土壓採臨界深度處之有效覆土壓以計算樁底極限端點支承力與樁身極限摩擦力。

倘基樁因施工因素造成樁底承載力無法完全發揮 (如：樁底沉泥無法清除)，可視有效樁底面積減少，在 CATii 中將樁底面積折減係數 α_b 設為小於 1 的數值可模擬此效果。

基礎開挖致使開挖面下方地層解壓，造成樁頂有效應力降低，此時可將 σ_ve'/σ_v' 設定為小於 1，倘不考慮有效應力降低則將 σ_ve'/σ_v' 設為 1。

註：σ_v' 為未解壓前之樁頂有效應力，σ_ve' 為開挖解壓後之樁頂有效應力。

排水地層同時含有 c' (c' ≠ 0) 及 ϕ' 時，以靜力學分析可選擇計算摩擦力 f_s 與底承力 q_b 之方式。

靜力學分析時僅考慮 ϕ' (規範建議選項)

$$\mathrm{f_s=Kσ_v'tanδ}$$ $$\mathrm{q_b=σ_v'N_q^*}$$

靜力學分析時 c' 及 ϕ' 皆考慮

$$\mathrm{f_s=αc'+Kσ_v'tanδ}$$ $$\mathrm{q_b=c'N_c^*+σ_v'N_q^*}$$

AISCS 說明受軸向壓力與彎矩共同作用之構材，應符合以下組合應力之規定，檢核 (H1-1) 及 (H1-2) 公式：

$$\mathrm{\frac{f_a}{F_a}+\frac{C_{mx}f_{bx}}{(1-f_a/F_{ex}')F_{bx}}+\frac{C_{my}f_{by}}{(1-f_a/F_{ey}')F_{by}}}\le1.0$$ $$\mathrm{\frac{f_a}{0.6F_y}+\frac{f_{bx}}{F_{bx}}+\frac{f_{by}}{F_{by}}}\le1.0$$

於 f_a/F_a ≤ 0.15 之情況下，則允許以 (H1-3) 公式取代上述之公式：

$$\mathrm{\frac{f_a}{F_a}+\frac{f_{bx}}{F_{bx}}+\frac{f_{by}}{F_{by}}}\le1.0$$

然於部分 f_a/F_a ≤ 0.15 條件下以 (H1-3) 公式檢核，增加型鋼長度反而增加強軸容許彎矩 M_xa (如上圖)，此時一律採用 AISCS (H1-1) 及 (H1-2) 公式則可避免此一情況 (如下圖)。